Research/Writings

My research interests are in homotopy theory, motivated from the chromatic perspective, and the tools I use are often computational. I have recently been interested in periodicity in motivic and equivariant stable homotopy theory, and I like to use the Adams spectral sequence to access periodic elements (although recently, I have had an eye towards the slice spectral sequence…). I have also written some user’s guides to some of my papers that you can check out here.

Preprints/Publications

• Real K-theory of equivariant classifying spaces, joint with Manyi Guo, Alex Waugh, and Albert Yang. In preparation.
  Abstract

  We compute the Atiyah Real K-theory of the classifying space for $C_2$-equivariant principal $\Sigma_2$-bundles. Using our computation, we produce a $C_2$-equivariant analogue of James periodicity.
• Exotic motivic self-maps of periodicity 1. In preparation.
  Abstract

  We construct finite motivic spectra with a $v_1$- and $w_1$-self-maps of periodicity 1 over $\mathbb{C}, \mathbb{R},$ and $\mathbb{F}_q$. The cofibers of these self-maps participate in splittings of many chromatically interesting motivic spectra.
• Splittings of truncated motivic Brown-Peterson cooperations algebras, joint with Sarah Petersen and Liz Tatum. Submitted. arxiv:2509.19542
  Abstract

  We construct spectrum-level splittings of $\text{BPGL}\langle 1\rangle\wedge \text{BPGL}\langle 1\rangle$ at all primes $p$, where $\text{BPGL}\langle 1 \rangle$ is the first truncated motivic Brown-Peterson spectrum. Classically, $\text{BP}\langle 1 \rangle \wedge \text{BP}\langle 1\rangle$ was first described by Kane and Mahowald in terms of Brown-Gitler spectra. This splitting was subsequently reinterpreted by Lellman and Davis-Gitler-Mahowald in terms of Adams covers. In this paper, we give motivic lifts of these splittings in terms of Adams covers, over the base fields $\mathbb{C}$, $\mathbb{R}$, and $\mathbb{F}_q$, where $\text{char}(\mathbb{F}_q)\neq p$. As an application, we compute the $E_1$-page of the $\text{BPGL}\langle 1 \rangle$-based Adams spectral sequence as a module over $\text{BPGL}\langle 1 \rangle$, both in homotopy and in terms of motivic spectra. We also record analogous splittings for $\text{BPGL}\langle 0 \rangle \wedge \text{BPGL} \langle 0 \rangle$.
• Rings of cooperations for Hermitian K-theory over finite fields. Submitted. arxiv:2509.02786, User’s Guide.
  Abstract

  We compute the ring of cooperations $\pi_{**}(\text{kq} \otimes \text{kq})$ for the very effective Hermitian K-theory over all finite fields $\mathbb{F}_q$ where $\text{char}(\text{F}_q) \neq 2$. To do this, we use the motivic Adams spectral sequence and show that all differentials are determined by the integral motivic cohomology of $\mathbb{F}_q$. As an application, we compute the $E_1$-page of the kq-resolution.
• On the ring of cooperations for real Hermitian K-theory. Submitted. arxiv:2506.16672, User’s Guide.
  Abstract

  Let $\text{kq}$ denote the very effective cover of the motivic Hermitian K-theory spectrum. We analyze the ring of cooperations $\pi_{**}(\text{kq} \otimes \text{kq})$ in the stable motivic homotopy category $\text{SH}(\mathbb{R})$, giving a full description in terms of Brown-Gitler comodules. To do this, we decompose the $E_2$-page of the motivic Adams spectral sequence and show that it must collapse. The description of the $E_2$-page is accomplished by a series of algebraic Atiyah-Hirzebruch spectral sequences which converge to the summands of the $E_2$-page. Along the way, we prove a splitting result for the very effective symplectic K-theory $\text{ksp}$ over any base field of characteristic not two.
• Toric double determinantal varieties, joint with Alexander Blose, Patricia Klein, and Owen McGrath. Published in Communications in Algebra 49 (2021), 7, 3085-3093. arxiv:2006.04191
  Abstract

  We examine Li's double determinantal varieties in the special case that they are toric. We recover from the general double determinantal varieties case, via a more elementary argument, that they are irreducible and show that toric double determinantal varieties are smooth. We use this framework to give a straighforward formula for their dimension. Finally, we use the smallest nontrivial toric double determinantal variety to provide some empirical evidence concerning an open problem in local algebra.

Writings

• Splittings and the algebraic Atiyah-Hirzebruch spectral sequence Expanded set of notes for preseminar talk at UW. PDF
• Galois descent and the Picard group of K-theory Notes for a talk in the UW Student AG Seminar. PDF
• The Adams spectral sequence and Hopf algebroids Notes for a talk in the DUBTOP seminar. PDF

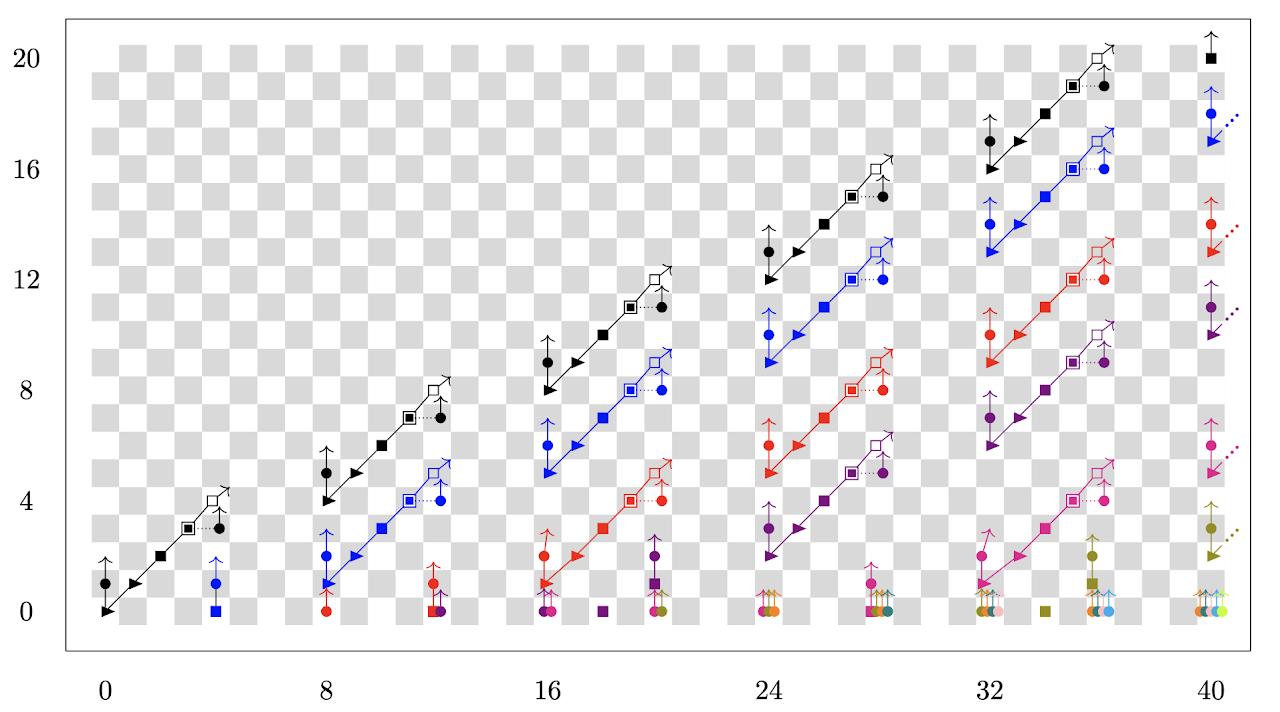The ring of cooperations $\pi_{**}(\text{kq} \otimes \text{kq})$ over $\mathbb{F}_3$.

Recent Talks

• Cooperations in motivic homotopy theory, JMM, January 2026. Slides
• Splittings and cooperations in motivic homotopy theory, University of Virginia Topology Seminar, November 2025
• Splittings and cooperations in motivic homotopy theory, University of Kentucky Topology Seminar, November 2025
• Higher Adams differentials and hidden extensions, eCHT Secondary Steenrod Algebra Reading Seminar, November 2025
• Splittings and cooperations in motivic homotopy theory, Duke University Geometry and Topology Seminar, October 2025
• Splittings of truncated motivic Brown-Peterson cooperations algebras, University of Colorado Boulder Homotopy Theory Seminar, September 2025
• On the ring of cooperations for real Hermitian K-theory, University of Michigan Geometry Seminar, September 2025
• Splittings and cooperations in motivic homotopy theory, University of Notre Dame Topology Seminar, September 2025
• On the ring of cooperations for real Hermitian K-theory, University of Washington Topology Seminar, June 2025